Leetcode 814. Binary Tree Pruning

We are given the head node root of a binary tree, where additionally every node's value is either a 0 or a 1.

Return the same tree where every subtree (of the given tree) not containing a 1 has been removed.

(Recall that the subtree of a node X is X, plus every node that is a descendant of X.)

Example 1:
Input: [1,null,0,0,1]
Output: [1,null,0,null,1]
 
Explanation: 
Only the red nodes satisfy the property "every subtree not containing a 1".
The diagram on the right represents the answer.

Example 2:
Input: [1,0,1,0,0,0,1]
Output: [1,null,1,null,1]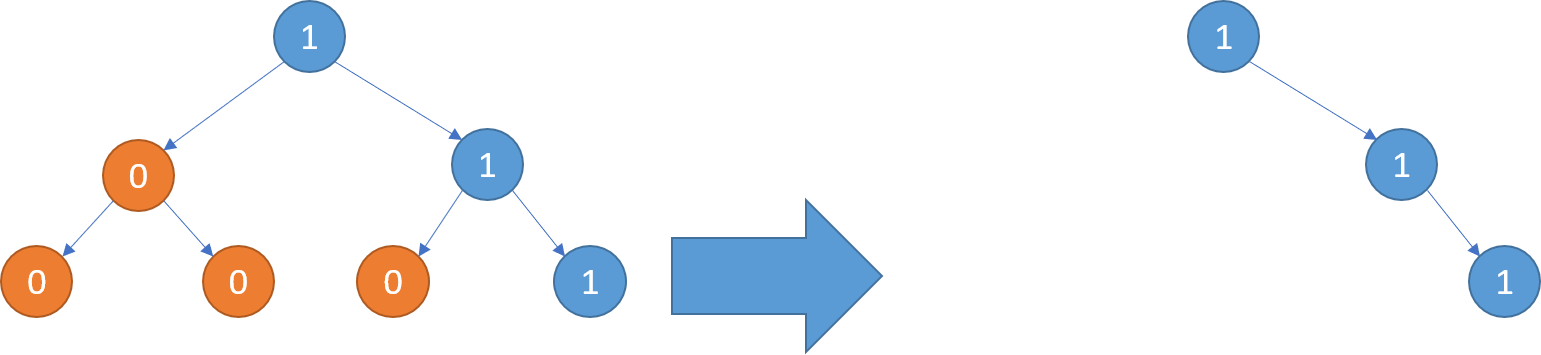

Example 3:
Input: [1,1,0,1,1,0,1,0]
Output: [1,1,0,1,1,null,1]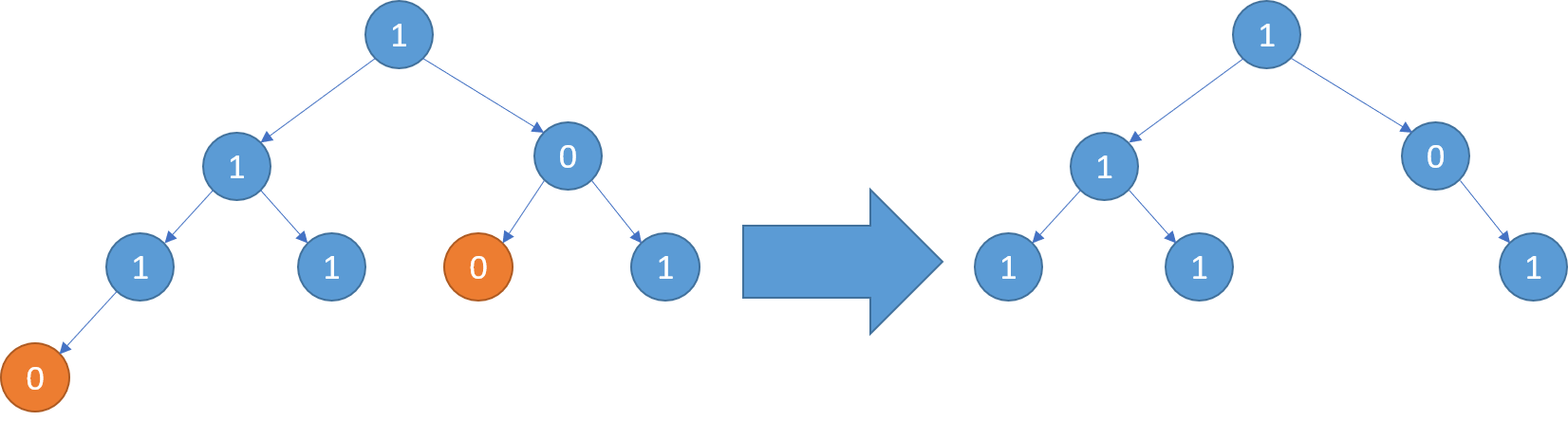

Note:

• The binary tree will have at most 100 nodes.
• The value of each node will only be 0 or 1.

Code (Java)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode pruneTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        
        root.left = pruneTree(root.left);
        root.right = pruneTree(root.right);
        
        if (root.val == 1 || root.left != null || root.right != null) {
            return root;
        }
        
        return null;
        
    }
}

Another solution:

Algorithm

We'll use a function containsOne(node) that does two things: it tells us whether the subtree at this nodecontains a 1, and it also prunes all subtrees not containing 1.

If for example, node.left does not contain a one, then we should prune it via node.left = null.

Also, the parent needs to be checked. If for example the tree is a single node 0, the answer is an empty tree.

Complexity Analysis

• Time Complexity: $O(N)$, where $N$ is the number of nodes in the tree. We process each node once.
• Space Complexity: $O(H)$, where $H$ is the height of the tree. This represents the size of the implicit call stack in our recursion.