Leetcode 802. Find Eventual Safe States

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph.  If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node.  More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe?  Return them as an array in sorted order.

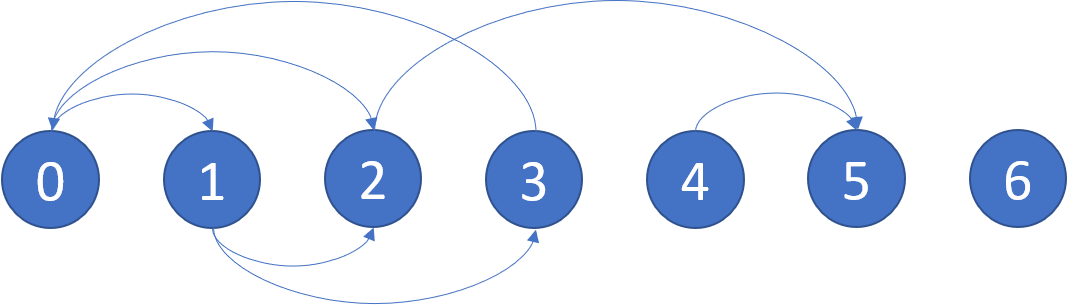
The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph.  The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Here is a diagram of the above graph.

Note:

• graph will have length at most 10000.
• The number of edges in the graph will not exceed 32000.
• Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

Solution:

The problem is actually asking if we can find a cycle in a graph. If yes, then all the nodes in the cycle are unstable. We can use DFS to find out a cycle in a graph. NOTE that we may do some pruning optimization.

Code (Java): -- TLE error

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        List<Integer> ans = new ArrayList<>();
        
        if (graph == null || graph.length == 0) {
            return ans;
        }
        
        int numOfNodes = graph.length;
        
        boolean[] stableNodes = new boolean[numOfNodes];
        // Init as true
        //
        for (int i = 0; i < numOfNodes; i++) {
            stableNodes[i] = true;
        }
        
        // DFS for each node and find cycle in a graph
        //
        for (int i = 0; i < numOfNodes; i++) {
            // Pruning. If the node is blacklisted, skip and go to next node
            //
            if (stableNodes[i] == false) {
                continue;
            }
            
            findCycleInGraph(graph, i, stableNodes);
        }
        
        // stableNodes is in sorted order
        //
        for (int i = 0; i < numOfNodes; i++) {
            if (stableNodes[i]) {
                ans.add(i);
            }
        }
        
        return ans;
    }
    
    private void findCycleInGraph(int[][] graph, int source, boolean[] stableNodes) {
        Set<Integer> visitedNodes = new HashSet<>();
        
        findCycleInGraphHelper(graph, source, stableNodes, visitedNodes);
    }
    
    private boolean findCycleInGraphHelper(int[][] graph, int source, boolean[] stableNodes, Set<Integer> visitedNodes) {
        // Check the cycle in the graph
        //
        if (visitedNodes.contains(source)) {
            addToBlackList(visitedNodes, stableNodes);
            return true;
        }
        
        // Add source node into the visited list
        //
        visitedNodes.add(source);
        
        // DFS the graph
        //
        boolean hasCycle = false;
        
        for (int neighbor : graph[source]) {
            hasCycle = findCycleInGraphHelper(graph, neighbor, stableNodes, visitedNodes);
            // pruning
            //
            if (hasCycle) {
                break;
            }
        }
        
        // Remove the node from the visited list
        //
        visitedNodes.remove(source);
        
        return hasCycle;
    }
    
    private void addToBlackList(Set<Integer> visitedNodes, boolean[] stableNodes) {
        Iterator it = visitedNodes.iterator();
        
        while (it.hasNext()) {
            int visitedNode = (int)it.next();
            stableNodes[visitedNode] = false;
        }
    }
}

A Slightly optimized solution:
In the previous solution, if we can find a cycle in a graph, then all the nodes in the cycle are unstable. So we don't need to traverse from that node again. Another optimization could be, if we cannot find a cycle after traversing all the paths, we can mark this node as stable. Then we don't need to check it again.

To implement this, we can use a black-white node. A node is black means the node is unstable, while the node is white means it's stable.

Code (Java):

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        List<Integer> ans = new ArrayList<>();
        
        if (graph == null || graph.length == 0) {
            return ans;
        }
        
        int numOfNodes = graph.length;
        
        // 2 is stable, 1 is unstable
        //
        int[] color = new int[numOfNodes];
        
        for (int i = 0; i < numOfNodes; i++) {
            // IF the color is 1 or 2, then skip
            //
            if (color[i] == 1 || color[i] == 2) {
                continue;
            }
            
            findCycleInGraph(graph, i, color);
        }
        
        // Construct result
        //
        for (int i = 0; i < numOfNodes; i++) {
            if (color[i] == 2) {
                ans.add(i);
            }
        }
        
        return ans;
    }
    
    private boolean findCycleInGraph(int[][] graph, int source, int[] color) {
        if (color[source] == 2) {
            return false;
        }
        
        if (color[source] == 1) {
           return true; 
        }
        
        color[source] = 1;
        
        for (int neighbor : graph[source]) {
            boolean hasCycle = findCycleInGraph(graph, neighbor, color);
            
            if (hasCycle) {
                return true;
            }
        }
        
        color[source] = 2;
        
        return false;
    }
}

Complexity Analysis

• Time Complexity: $O(N + E)$, where $N$ is the number of nodes in the given graph, and $E$ is the total number of edges.
• Space Complexity: $O(N)$ in additional space complexity.